我们在 JavaScript 里执行 0.1 + 0.2，会得到下面这个结果：

> 0.1 + 0.2
> 0.30000000000000004

为什么在 Javascript 中 0.1 + 0.2 !== 0.3 呢？为了解释这个问题，我们首先需要明白，计算机是怎么存储数字的

计算机是怎么存储数字的

计算机是用二进制来存储数据的，同样的，我们平常使用的十进制的数字也需要转换成二进制的数字来存储。

十进制与二进制的转换

十进制正整数转二进制

十进制整数转二进制采用的是 除 2 取余法 ，比如数字 8 转二进制的过程如下图：

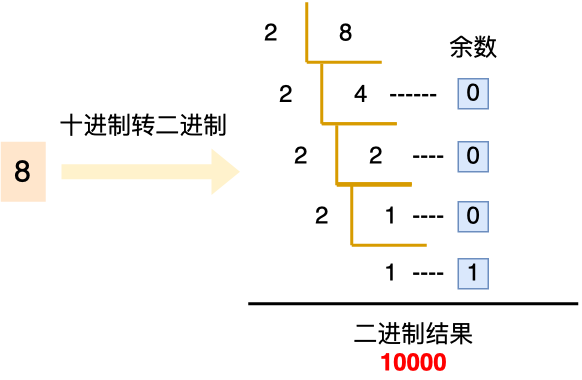
我们以 int 类型的数字作为例子，int 类型是 32 位的，其中最高位是作为「符号标志位」，正数的符号位是 0，负数的符号位是 1，剩余的 31 位则表示二进制数据。

那么，对于 int 类型的数字 1 的二进制数表示如下：

十进制负整数转二进制

而负数就比较特殊了点，负数在计算机中是以 补码 表示的，所谓的补码就是把正数的二进制全部取反再加 1，比如 -1 的二进制是把数字 1 的二进制取反后再加 1，如下图：

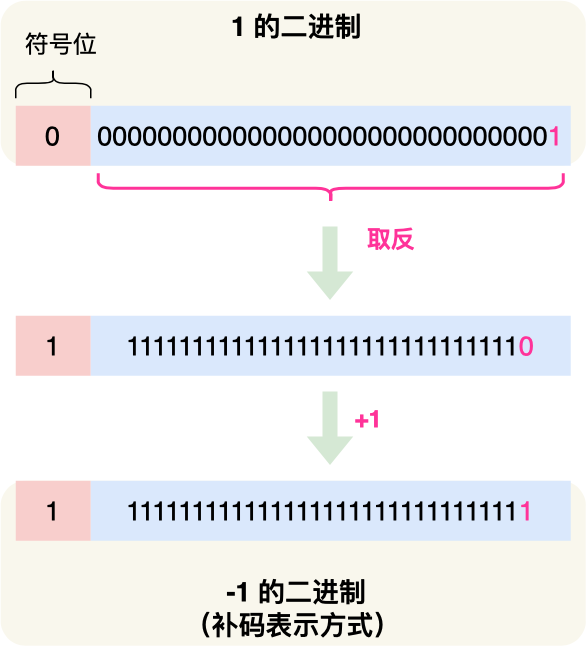
十进制小数转二进制

小数部分的转换不同于整数部分，它采用的是 乘 2 取整法 ，将十进制中的小数部分乘以 2 作为二进制的一位，然后继续取小数部分乘以 2 作为下一位，直到不存在小数为止。

我们就以 8.625 转二进制作为例子，转二进制的过程如下图：

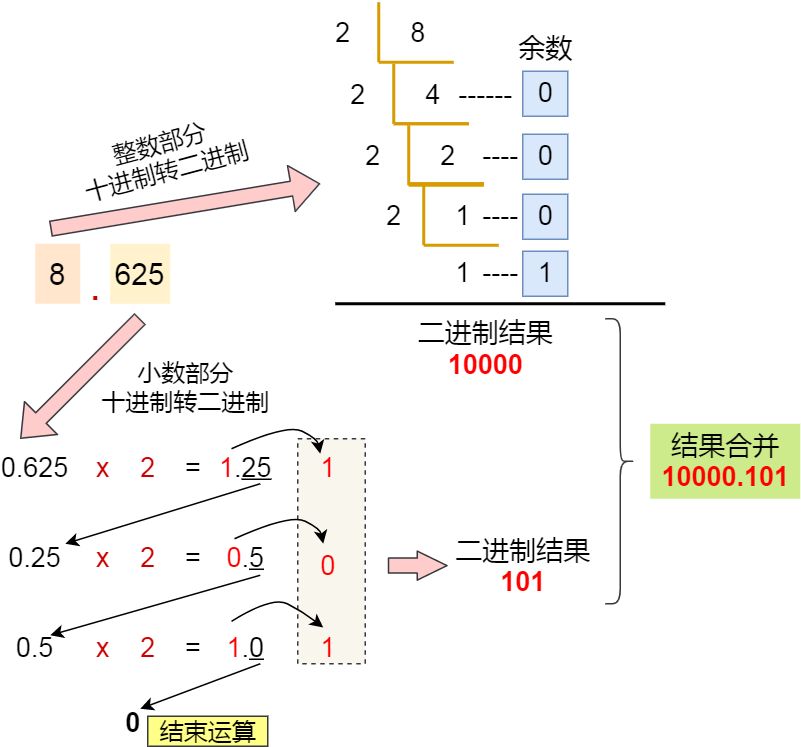
最后把「整数部分 + 小数部分」结合在一起后，其结果就是 1000.101。

但是，并不是所有小数都可以用二进制表示，前面提到的 0.625 小数是一个特例，刚好通过乘 2 取整法的方式完整的转换成二进制，如果我们用相同的方式，来把 0.1 转换成二进制，过程如下：

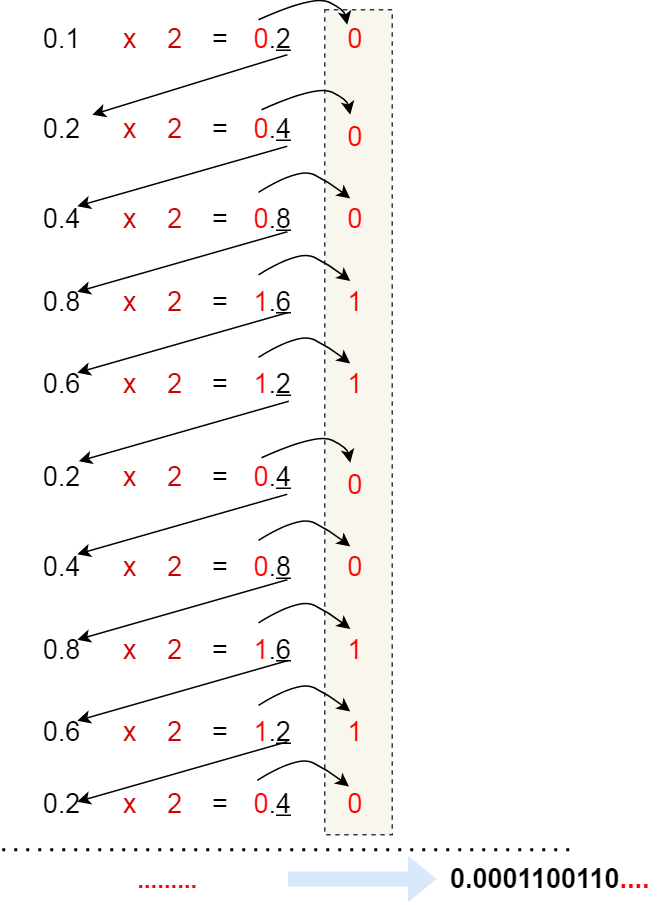
可以发现，0.1 的二进制表示是无限循环的，由于计算机的资源是有限的，所以是没办法用二进制精确的表示 0.1，只能用「近似值」来表示，就是在有限的精度情况下，最大化接近 0.1 的二进制数，于是就会造成精度缺失的情况。

二进制小数转十进制

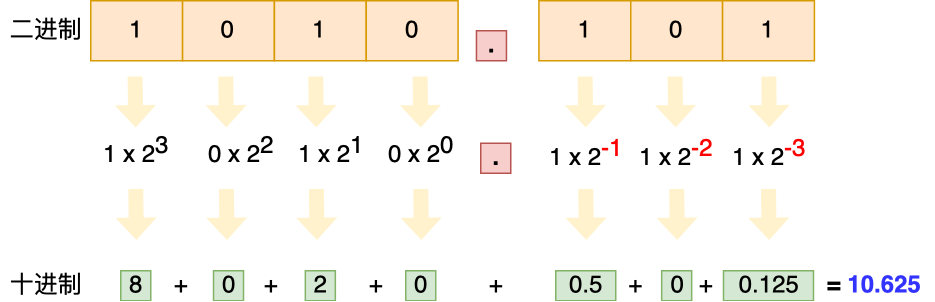
对于二进制小数转十进制时，需要注意一点，小数点后面的指数幂是负数，比如二进制 0.1 转成十进制就是 2^(-1)，也就是十进制 0.5，二进制 0.01 转成十进制就是 2^-2，也就是十进制 0.25，以此类推。

举个例子，二进制 1010.101 转十进制的过程，如下图：

定点数与浮点数

1010.101 这种二进制小数是 定点数 形式，代表着小数点是定死的，不能移动，如果你移动了它的小数点，这个数就变了， 就不再是它原来的值了。

然而，计算机并不是这样存储的小数的，计算机存储小数的采用的是 浮点数 ，名字里的「浮点」表示小数点是可以浮动的，比如 1000.101 这个二进制数，可以表示成 1.000101 x 2^(-3)，类似于数学上的科学记数法。

因此，如果二进制要用到科学记数法，同时要规范化，那么不仅要保证基数为 2，还要保证小数点左侧只有 1 位，而且必须为 1，所以通常将 1000.101 这种二进制数，表示成 1.000101 x 2^(-3)，其中，最为关键的是 000101 和 -3 这两个东西，它就可以包含了这个二进制小数的所有信息，000101 称为 尾数 ，即小数点后面的数字，-3 称为 指数，指定了小数点在数据中的位置。

现在绝大多数计算机使用的浮点数，一般采用的是 IEEE 制定的国际标准，这种标准形式如下图：

这三个重要部分的意义如下：

• 符号位：表示数字是正数还是负数，为 0 表示正数，为 1 表示负数；
• 指数位：指定了小数点在数据中的位置，指数可以是负数，也可以是正数，指数位的长度越长则数值的表达范围就越大；
• 尾数位：小数点右侧的数字，也就是小数部分，比如二进制 1.0011 x 2^(-2)，尾数部分就是 0011，而且尾数的长度决定了这个数的精度，因此如果要表示精度更高的小数，则就要提高尾数位的长度；
• 用 32 位来表示的浮点数，则称为 单精度浮点数，也就是我们编程语言中的 float 变量，而用 64 位来表示的浮点数，称为 双精度浮点数，也就是 double 变量，它们的结构如下：

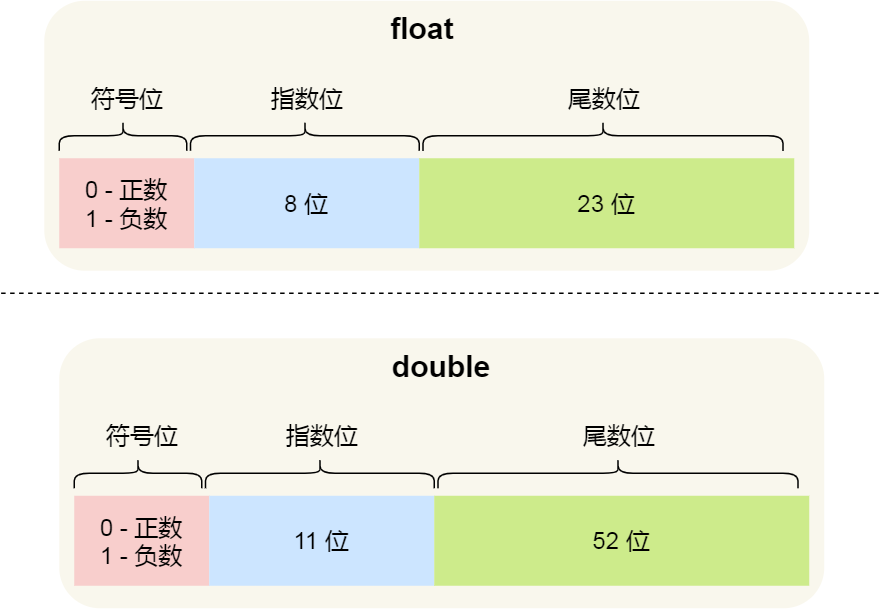
可以看到：

• double 的尾数部分是 52 位，float 的尾数部分是 23 位，由于同时都带有一个固定隐含位（这个后面会说），所以 double 有 53 个二进制有效位，float 有 24 个二进制有效位，所以所以它们的精度在十进制中分别是 log10(2^53) 约等于 15.95 和 log10(2^24) 约等于 7.22 位，因此 double 的有效数字是 15~16 位，float 的有效数字是 7~8 位，这些是有效位是包含整数部分和小数部分；
• double 的指数部分是 11 位，而 float 的指数位是 8 位，意味着 double 相比 float 能表示更大的数值范围；

二进制小数转二进制浮点数

那二进制小数，是如何转换成二进制浮点数的呢？我们就以 10.625 作为例子，看看这个数字在 float 里是如何存储的。

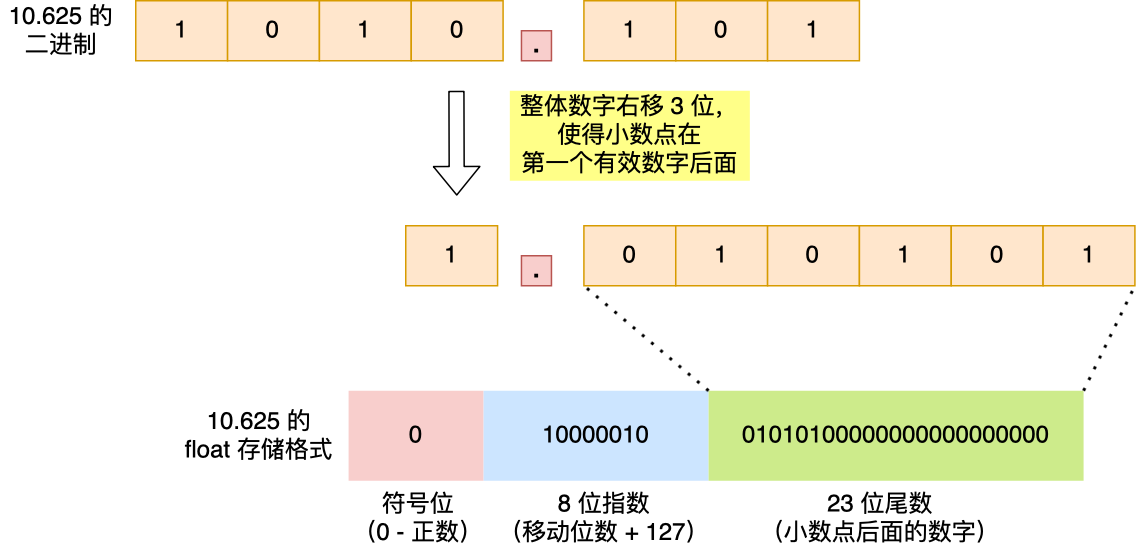
首先，我们计算出 10.625 的二进制小数为 1010.101，然后把小数点，移动到第一个有效数字后面，即将 1010.101 右移 3 位成 1.010101，右移 3 位就代表 +3，左移 3 位就是 -3，float 中的「指数位」就跟这里移动的位数有关系，把移动的位数再加上「偏移量」，float 的话偏移量是 127，相加后就是指数位的值了，即指数位这 8 位存的是 10000010（十进制 130），因此你可以认为「指数位」相当于指明了小数点在数据中的位置。

1.010101 这小数点右侧的数字就是 float 里的「尾数位」，由于尾数位是 23 位，则后面要补充 0，所以最终尾数位存储的数字是 01010100000000000000000。

在算指数的时候，你可能会有疑问为什么要加上偏移量呢？

前面也提到，指数可能是正数，也可能是负数，即指数是有符号的整数，而有符号整数的计算是比无符号整数麻烦的，所以为了减少不必要的麻烦，在实际存储指数的时候，需要把指数转换成无符号整数，float 的指数部分是 8 位，IEEE 标准规定单精度浮点的指数取值范围是 -126 ~ +127，于是为了把指数转换成无符号整数，就要加个偏移量，比如 float 的指数偏移量是 127，这样指数就不会出现负数了。

比如，指数如果是 8，则实际存储的指数是 8 + 127 = 135，即把 135 转换为二进制之后再存储，而当我们需要计算实际的十进制数的时候，再把指数减去偏移量即可。

同时，因为 IEEE 标准规定，二进制浮点数的小数点左侧只能有 1 位，并且还只能是 1，既然这一位永远都是 1，那就可以不用存起来了，于是就让 23 位尾数只存储小数部分，电路在计算时会自动把这个 1 加上，这样就可以节约 1 位的空间，尾数就能多存一位小数，相应的精度就更高了一点。这 1 位就是上面提到的固定隐含位。

二进制浮点数转十进制

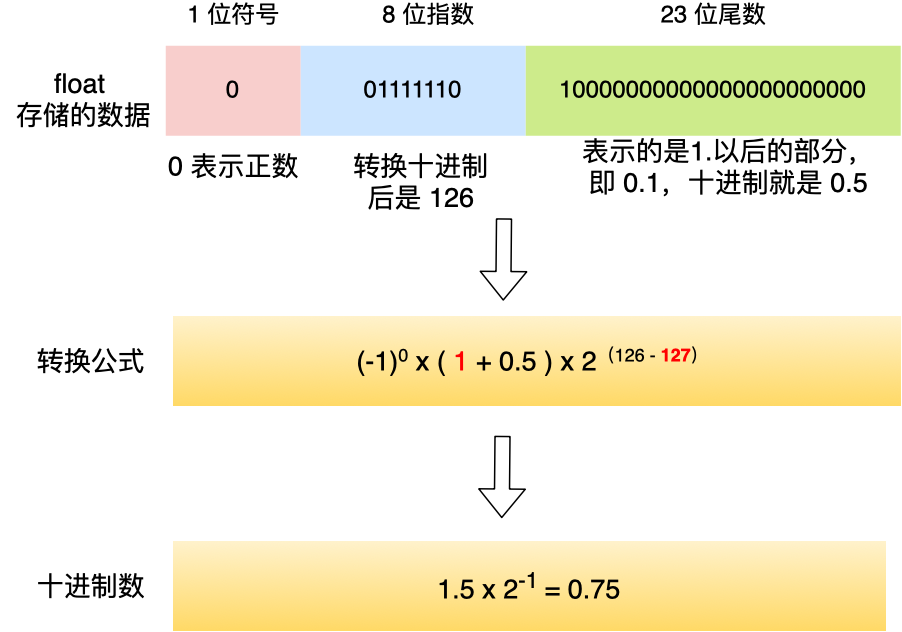
那么，对于我们在从 float 的二进制浮点数转换成十进制时，要考虑到这个隐含的 1，转换公式如下：

举个例子，我们把下图这个 float 的数据转换成十进制，过程如下：

为什么 0.1 + 0.2 !== 0.3

前面提到过，并不是所有小数都可以用「完整」的二进制来表示的，比如十进制 0.1 在转换成二进制小数的时候，是一串无限循环的二进制数，计算机是无法表达无限循环的二进制数的，毕竟计算机的资源是有限。

因此，计算机只能用「近似值」二进制浮点数来表示该十进制小数，那么意味着计算机存放的小数可能不是一个真实值，现在基本都是用 IEEE 754 规范的单精度浮点类型或双精度浮点类型来存储小数的，根据精度的不同，近似值也会不同。

那计算机是以一个怎么样的二进制浮点数来存储十进制的 0.1 呢？可以使用 binaryconvert 在线转换一下。

得到 0.1 的二进制浮点数是 00111101 11001100 11001100 11001101 转换成十进制的结果是 0.100000001490116119384765625

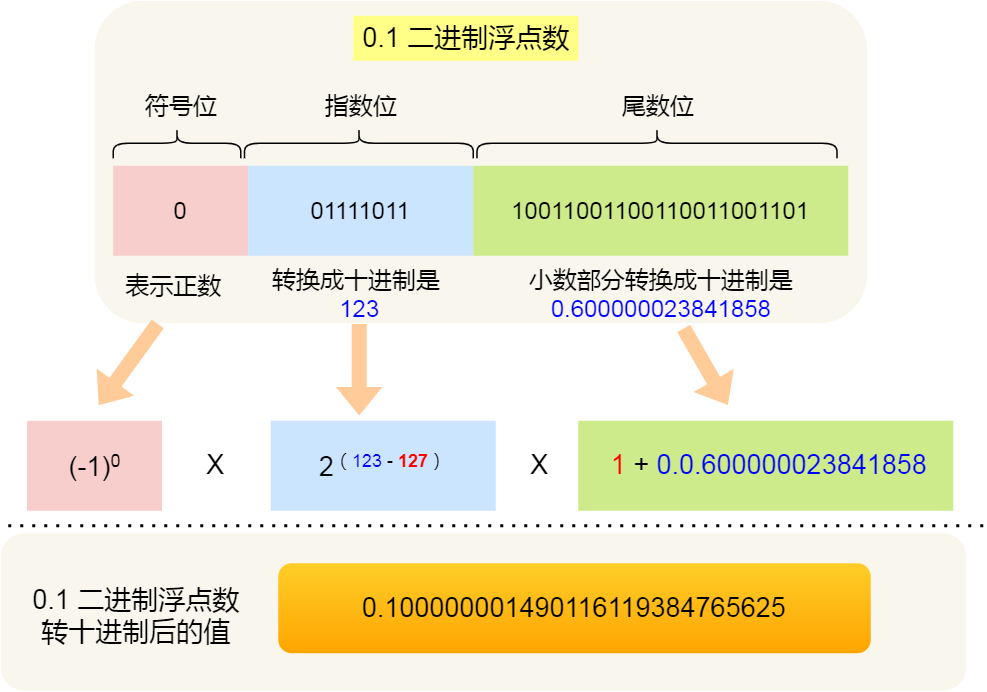
0.2 的二进制浮点数是 00111110 01001100 11001100 11001101 转换成十进制的结果是 0.20000000298023223876953125

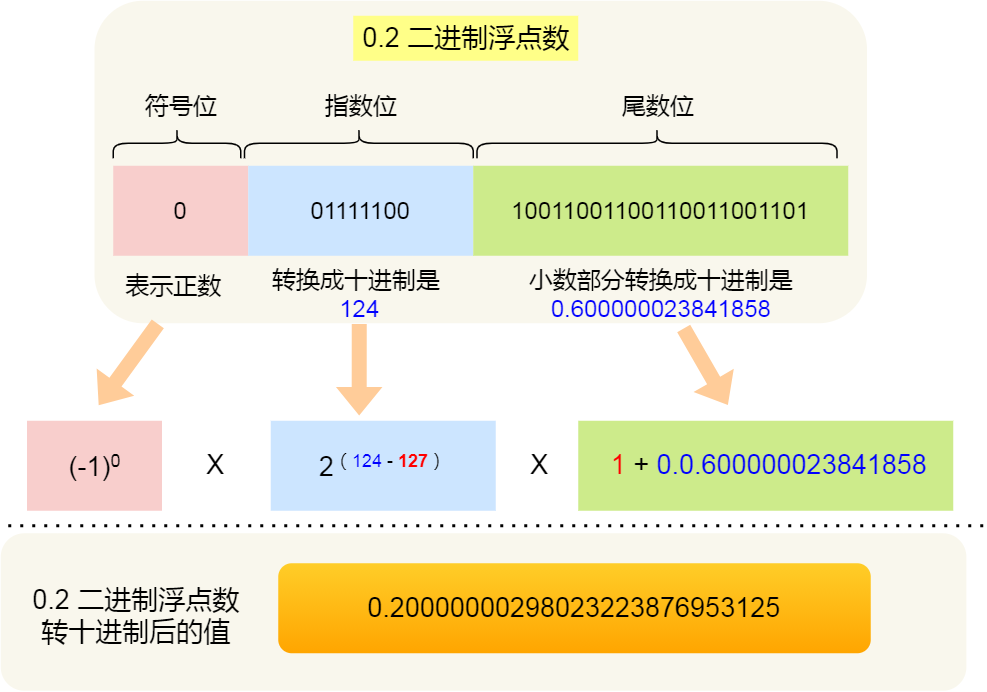
这两个结果相加就是 0.300000004470348358154296875

所以，你会看到在计算机中 0.1 + 0.2 并不等于完整的 0.3，这主要是因为有的小数无法用「完整」的二进制来表示，所以计算机里只能采用近似数的方式来保存，那两个近似数相加，得到的必然也是一个近似数。

因为 JavaScript 对于数字都是使用 IEEE 754 标准下的双精度浮点类型来存储的，所以在 JavaScript 里执行 0.1 + 0.2，你会得到 0.30000000000000004 这个结果。